반응형
Graph Traversal (그래프 순회)
- 대표적인 두 가지 방법
- DFS (Depth-First Search)
- BFS (Breadth-First Search)
- 동일한 Tree를 각각 DFS/BFS로 방문하기
- DFS : 깊이 먼저, 스택 (Stack) 자료구조 활용
- BFS : 너비 먼저, 큐 (Queue) 자료구조 활용
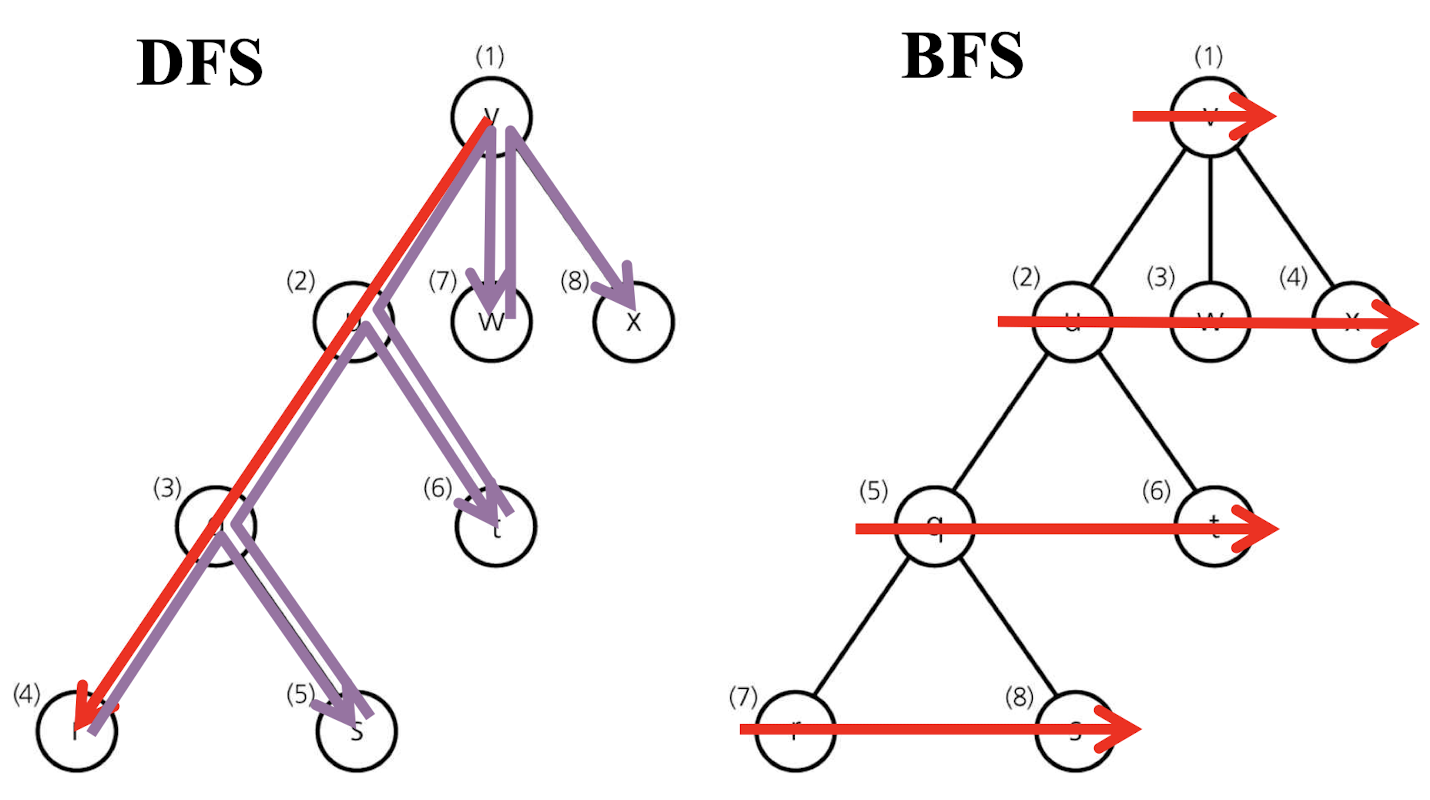
깊이 우선 탐색 (Depth-First Search; DFS)
- (1) 정점 i를 방문한다.
- (2) 정점 i에 인접한 정점 중에서 아직 방문하지 않은 정점이 있으면, 이 정점들을 모두 스택에 저장한다.
- (3) 스택에서 정점을 삭제하여 새로운 i를 설정하고, 단계 (1)을 수행한다.
- (4) 스택이 공백이 되면 연산을 종료한다.
DFS(s) {
// s 는 시작 정점
for (i←0; i<n; i ← i +1) do {
visited[i] ← false; // 모든 정점을 방문하지 않은 것으로 마크
}
stack ← createStack(); // 방문할 정점을 저장하는 스택
push(stack, s); // 시작 정점 s를 스택에 저장
while (not isEmpty(stack)) do { // 스택이 공백이 될 때까지 반복 처리
j ← pop(stack);
if (visited[j] = false) then { // 정점 j를 아직 방문하지 않았다면
visit j; // 직접 j를 방문하고
visited[j] ← true; // 방문 한 것으로 마크
for (each k ∈ adjacency(j)) do { // 정점 j에 인접한 정점 중에서
if (visited[k] = false) then // 아직 방문하지 않은 정점들을
push(stack, k); // 스택에 저장
} // end for
} // end if
} // end while
} end DFS()너비 우선 탐색 (Breadth-First Search; BFS)
- (1) 정점 i를 방문한다.
- (2) 정점 i에 인접한 정점 중에서 아직 방문하지 않은 정점이 있으면, 이 정점들을 모두 큐에 저장한다.
- (3) 큐에서 정점을 삭제하여 새로운 i를 설정하고, 단계 (1)을 수행한다.
- (4) 큐가 공백이 되면 연산을 종료한다.
BFS(s) {
// s 는 시작 정점
for (i←0; i<n; i ← i +1) do {
visited[i] ← false; // 모든 정점을 방문하지 않은 것으로 마크
}
visited[s] ← true;
queue ← creatQ(); // 방문할 정점을 저장하는 큐
enqueue(queue, s); // 시작 정점 s를 큐에 저장
while (not isEmpty(queue)) do { // 큐가 공백이 될 때까지 반복 처리
j ← dequeue(queue);
visit j; // 직접 j를 방문
for (each k ∈ adjacency(j)) do { // 정점 j에 인접한 정점 중에서
if (visited[k] = false) then { // 아직 방문하지 않은 정점들을
enqueue(queue, k); // 큐에 저장
visited[k] ← true; // 방문 한 것으로 마크
} // end if
} // end for
} // end while
} end BFS()반응형
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] 시간복잡도와 Master Theorem - 연습문제 (0) | 2023.09.23 |
|---|---|
| [알고리즘] 시간복잡도와 Master Theorem (0) | 2023.09.23 |
| [알고리즘] 허프만 인코딩 (Huffman encoding) - 파일 압축 알고리즘 (0) | 2022.06.14 |
| [알고리즘] 공개 키 암호화 시스템 - RSA(Rivest-Shamir-Adleman) 암호화 알고리즘 (0) | 2022.06.14 |
| [알고리즘] TSP (Traveling Salesperson Problem, 외판원 문제) (0) | 2022.06.14 |
