반응형
스트링 편집거리 (Levenshtein Distance)
- 두 스트링의 유사도를 측정하기 위해 사용
- Levenshtein Distance(LD)라고도 함
- 원래의 스트링을 𝑆(source), 편집하고자 하는 목표 스트링을 𝑇(target), 각각의 문자열의 길이를 𝑚,𝑛
- 𝛿_𝐼는 삽입 연산의 비용
- 𝛿_𝐷는 삭제 연산의 비용
- 𝛿_S는 교환 연산의 비용
- 편집 거리 : 𝑆를 𝑇로 변환하는데 필요한 삽입,삭제,대치연산의 최소 비용
- 𝑆 = “test”, 𝑇=“test” → LD(𝑆, 𝑇) = 0
- 𝑆 = “test”, 𝑇=“tent” → LD(𝑆, 𝑇) = 1
- 편집 거리가 커질수록, 두 스트링의 유사도는 낮아지게 됨
- 𝐷[𝑖][𝑗]를 𝑆=𝑠1𝑠2 ...𝑠𝑗와 𝑇=𝑡1𝑡2 ...𝑡𝑖 사이의 편집 거리라고 할 때, 𝐷[𝑖][𝑗]의 점화식 (Recursive Property)은 아래와 같다.

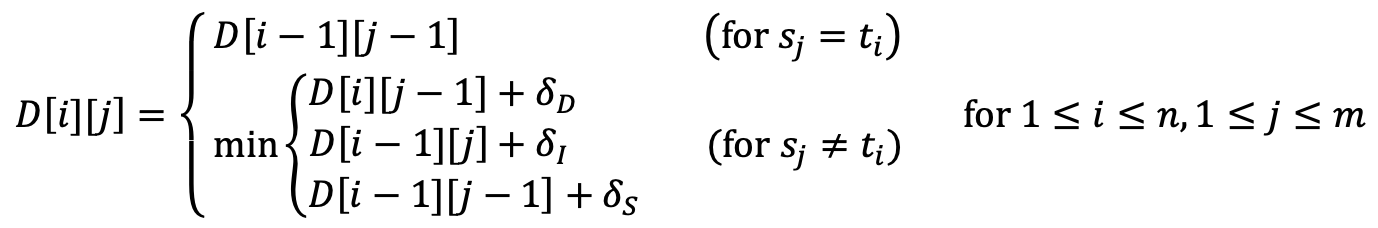
실습 및 코드는 아래 GitHub를 참고해주세요!
GitHub - oneonlee/Computer-Science: Introduction to Computer Science
Introduction to Computer Science. Contribute to oneonlee/Computer-Science development by creating an account on GitHub.
github.com
반응형
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] 최적 이진 탐색트리 (Optimal BST) (0) | 2022.06.14 |
|---|---|
| [알고리즘] 연쇄 행렬 곱셈 (Matrix-chain Multiplication) (0) | 2022.06.14 |
| [알고리즘] 0-1 Knapsack Problem (배낭 문제) (0) | 2022.06.14 |
| [알고리즘] Graph (그래프) 용어와 표현 방법, 종류와 예시 (0) | 2022.06.14 |
| [알고리즘] 최단 경로 알고리즘 비교 (Shortest Path Algorithms) (0) | 2022.06.14 |
