반응형
P vs. NP vs. NP-hard vs. NP-complete
- P
- 다항시간 내에 풀 수 있는 문제
- 또는 다차시간 알고리즘을 찾은 문제
- NP
- 다항시간 내에 답이 맞았는지 틀렸는지 확인해줄 수 있는 문제 (verification)
- 또는 다루기 힘들다고 증명되지 않았고, 다차시간 알고리즘도 찾지 못한 문제
- NP-hard
- 아무리 답을 추측해도 그 답이 맞았는지 틀렸는지 확인이 어려운 문제 (예 : 최적화 문제)
- NP-complete
- NP-hard임과 동시에 NP인 문제, 즉 모든 NP 문제를 Polynomial-Time Reduction (다항식 시간 변환)시킨 문제가 다시 NP가 될 때, 그 문제를 'NP-complete 문제'라고 부른다.
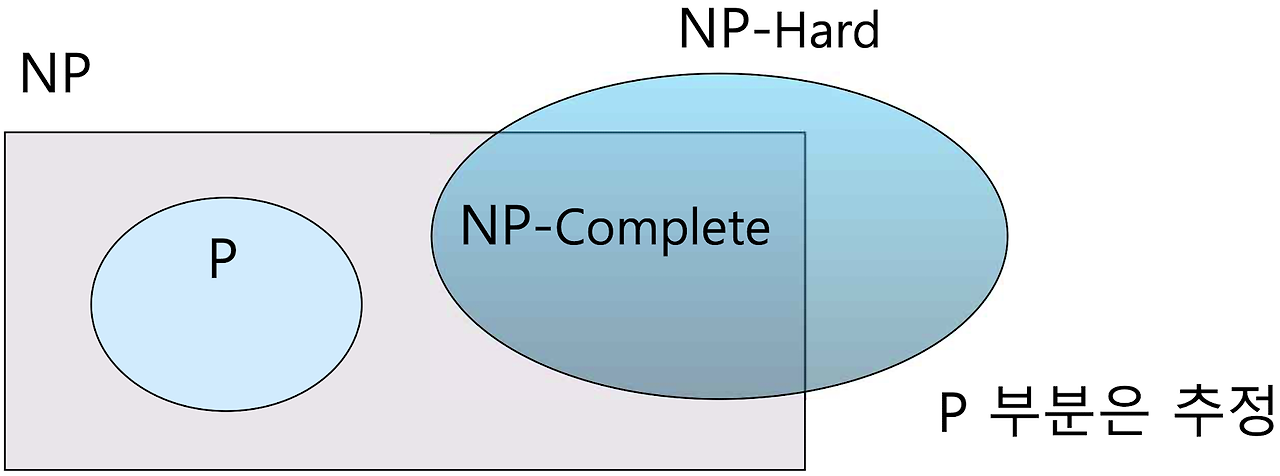
NP-hard
- NP-hard에 속하는 문제는?
- 모든 NP-complete은 NP-hard문제이다.
- NP-hard에 속하지 않는 문제는?
- 아직 모름. 어떤 문제가 NP-hard가 아니라고 증명하게 된다면
P ≠ NP임을 증명하게 되는 것.
- 아직 모름. 어떤 문제가 NP-hard가 아니라고 증명하게 된다면
- 다항시간 알고리즘을 발견한 문제는 NP-hard가 아닐지도 모름.
- 다항시간 알고리즘이 있는 어떤 문제가 NP-hard임을 증명하면
P = NP임을 증명하게 되는 것.
- 다항시간 알고리즘이 있는 어떤 문제가 NP-hard임을 증명하면
NP-complete
어떤 문제가 NP-complete인지 증명하기 위한 과정
만일,
- (1) 문제 B가 NP에 속하고
- (2) NP에 속해 있는 모든 다른 문제 A에 대해
A ≤ ₚB이면 B는 NP-complete이다. (NP-complete의 정의)- (2) 또는 잘 알려진 NP-complete 문제 A에 대해
A ≤ ₚB이면 B는 NP-complete이다. (Cook의 정리)
- (2) 또는 잘 알려진 NP-complete 문제 A에 대해
Polynomial-Time Reduction (다항식 시간 변환)
- 문제 A의 사례 α를 문제 B의 사례 β로 바꾸되 아래 성질을 만족하면 polynomial-time reduction이라 하고, 이를
α ≤ ₚβ로 표기한다- (1) 변환은 다항식 시간에 이루어진다
- (2) 두 사례의 답은 일치한다
반응형
'Computer Science > Algorithm' 카테고리의 다른 글
| [알고리즘] 시간복잡도와 Master Theorem - 연습문제 (0) | 2023.09.23 |
|---|---|
| [알고리즘] 시간복잡도와 Master Theorem (0) | 2023.09.23 |
| [Graph Traversal 알고리즘] DFS vs BFS (0) | 2022.10.18 |
| [알고리즘] 허프만 인코딩 (Huffman encoding) - 파일 압축 알고리즘 (0) | 2022.06.14 |
| [알고리즘] 공개 키 암호화 시스템 - RSA(Rivest-Shamir-Adleman) 암호화 알고리즘 (0) | 2022.06.14 |
